Mensuration Formula
Mensuration Formula: Mensuration, a fundamental branch of mathematics, is dedicated to the measurement and analysis of various geometric figures and shapes. It involves the calculation of areas, volumes, etc of shapes. These formulas provide efficient shortcuts to calculate areas, volumes, and other geometric measurements swiftly and accurately. Mensuration is one of the most essential and scoring topics in the quantitative aptitude section of the exam. In order to excel in this topic, you must know the formulas and concepts used to solve the questions. This article delves into the essential foundational mathematical mensuration formulas, providing thorough explanations to aid in your understanding and application.
What are 2D and 3D shapes?
- 2D Shapes- In geometry, a two-dimensional shape is a flat plane figure or a shape that has only two dimensions i.e. length and width. Two-dimensional or 2-D shapes do not possess any thickness and can be measured in only two faces. Only the area and perimeter of 2D shapes can be calculated.
- 3D Shapes- A three-dimensional shape is where the figure has three dimensions namely length, width, and thickness. We calculate volume, curved surface area, and the total surface area of 3D shapes.
Mensuration Formula of 2D Shapes
Check out the formula for the area and perimeter of some of the 2D shapes:
| Shape | Area (Square units) | Perimeter (units) |
|---|---|---|
| Square | a² | 4a |
| Rectangle | l × b | 2 ( l + b) |
| Circle | πr² | 2 π r |
| Scalene Triangle | √[s(s−a)(s−b)(s−c)],
Where, s = (a+b+c)/2 |
a+b+c |
| Isosceles Triangle | ½ × b × h | 2a + b |
| Equilateral Triangle | (√3/4) × a² | 3a |
| Right Angle Triangle | ½ × b × h | b + hypotenuse + h |
| Rhombus | ½ × d1 × d2 | 4 × side |
| Parallelogram | b × h | 2(l+b) |
| Trapezium | ½ h(a+b) | a+b+c+d |
Mensuration Formula of 3D Shapes
Check out the formula for some of the 3D shapes in geometry:
| Shape | Volume (Cubic units) | Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units) |
Total Surface Area (TSA) (Square units) |
|---|---|---|---|
| Cube | a³ | 4 a² | 6 a² |
| Cuboid | l × b × h | 2 h (l + b) | 2 (lb +bh +hl) |
| Sphere | (4/3) π r³ | 4 π r² | 4 π r² |
| Hemisphere | (⅔) π r³ | 2 π r² | 3 π r² |
| Cylinder | π r² h | 2π r h | 2πrh + 2πr² |
| Cone | (⅓) π r² h | π r l | πr (r + l) |
Mensuration Formulas in Detail
Mensuration Questions
Q1. The radius of a cylinder is 10 cm and the height is 4 cm. The number of centimeters that may be added either to the radius or to the height to get the same increase in the volume of the cylinder is :
(a) 5
(b) 4
(c) 25
(d) 16
Ans. (a)
Sol.
Let ‘a’ cm is added in radius and height
π(10+a)²4 = π (10)² (4 +a)
(10+a)²4 = 10² (4 +a)
⇒ a = 5 cm
Q2. PQRS is a rectangle. The ratio of the sides PQ and QR is 3: 1. If the length of the diagonal PR is 10 cm, then what is the area (in cm²) of the rectangle?
(a) 15
(b) 30
(c) 45
(d) 20
Ans.(b)
Sol.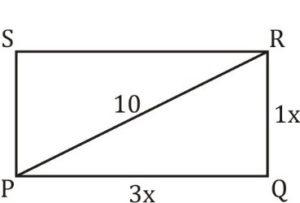
PQRS is a rectangle
PR = 10 given
PQ : QR = 3 : 1
In ∆PQR
9x² + x² = 100
10x² = 100
x = √10
Area of rectangle = 3x × 1x
= 3x²
= 3 × 10
= 30
Q3. The base of a prism is in the shape of an equilateral triangle. If the perimeter of the base is 18 cm and the height of the prism is 20 cm, then what is the volume (in cm³) of the prism?
(a) 180√3
(b) 30√6
(c) 60√2
(d) 120√3
Ans. (A)
Sol.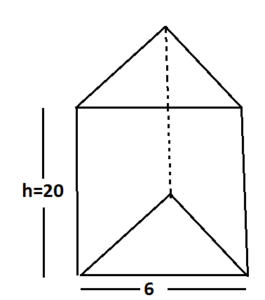
Given:-
Perimeter = 18 &height=20
Hence ,Side = 6
The volume of prism = area of base × height
= √3/4×6 × 6 × 20
V = 180√3 cm3
Q4. The height of a cone is 24 cm and the area of the base is 154 cm². What is the curved surface area (in cm²) of the cone?
(a) 484
(b) 550
(c) 525
(d) 515
Ans.(B)
Sol. Area of base = 154
πr² = 154
22/7×r^2=154
r = 7
Height = 24
Radius = 7
Slant height(ℓ) = √(h²+r² )
ℓ =√(24²+7² )
ℓ=25
C.S.A. = πrℓ
= 22/7×7×25
C.S.A. ⇒ 550 cm²
Q5. A right circular solid cylinder has a radius of the base of 7 cm and height is 28 cm. It is melted to form a cuboid such that the ratio of its side is 2 : 3: 6. What is the total surface area (in cm²) cuboid?
(a)72 ∛(( (1078)²)/(9²))
(b) ∛(2156/9)
(c) ∛(2148/3)
(d) ∛(2048/3)
Ans. (A)
Sol. According to the question, a cylinder is transforming into a cuboid as shown in the figure below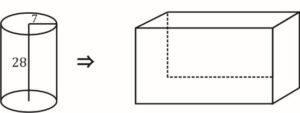
The volume of cylinder = volume of a cuboid
22/7×7×7×28=2x×3x×6x
x^3=1078/9 ⇒x=∛(1078/9)
T. Surface area of cuboid = 2 [ℓb + bh + hℓ]
=2×(1078/9)^(2/3) [2×3+3×6+6×2]
T.S.A.=72×(1078/9)^(2/3)
Q6. ABCDEF is a regular hexagon. What is the ratio of the area of triangle ACE and the area of triangle AEF?
(a) 6: 1
(b) 4: 1
(c) 3: 1
(d) 5: 1
Ans.(c)
Sol.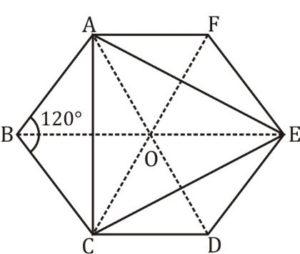
Given is a regular hexagon
In a regular hexagon, there are 6 equilateral triangles as shown by the dotted line
Area of ∆ACE = 1/2×[Area of 6 equilateral triangles]
= 3 equilateral triangles.
Area of ∆AEF = 1/2×[Area of 2 equilateral ∆]
= 1 equilateral triangle.
Hence ratio of
Area ACE : Area AEF = 3 : 1
Numerically proved
Let the length of the side of the hexagon = 12
Interior angle ∠ABC = ((x–2)×180)/n = ((6–2)×180)/6 = 120
Area of ∆ABC = 1/2×AB×BC×sin120
=1/2×12×12×cos30
Area of ∆ABC = 36√3
Similarly
Area ∆CDE = Area ∆AEF = 36√3
Area of hexagon = 6×√3/4×12×12 = 216√3
Area of ACE = Area of hexagon – [Area of ∆ABC + ∆CDE + ∆AEF]
= 216√3 –108√3
= 108√3
∴ Area of ACE: Area of AEF = 108√3 ∶36√3
= 3: 1
Q7. ABCD is a trapezium. Sides AB and CD are parallel to each other. AB = 6 cm, CD = 18 cm, BC = 8 cm and AD = 12 cm. A line parallel to AB divides the trapezium into two parts of an equal perimeter. This line cuts BC at E and AD at F. If BE/EC = AF/FD, then what is the value of BE/EC?
(a) 1/2
(b) 2
(c) 4
(d) 1/4
Ans.(c)
Sol.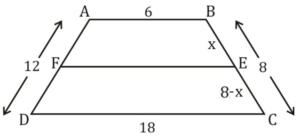
All given values are shown in the diagram
Let BE = x then EC = 8 – x
BE/EC=AF/FD (condition given)
Reverse the given condition & add 1 on both sides
EC/BE+1=FD/AF+1
(EC+BE)/BE=(FD+AF)/AF⇒BC/BE=AD/AF …(i)
Put values in eq. (i) → 8/x=12/AF AF=3x/2 & FD=12–3x/2
Now perimeter FABE = FECD
FA + AB + BE + FE = EC + CD + DF + FE
3x/2+6+x=8 –x+18+(12–3x/2)
5x = 32
x=32/5=BE, hence EC=8 –32/5=8/5
∴ BE/EC=(32/5)/(8/5)=4
Source link


