Heights and Distances are important topics in Quantitative Aptitude section of Competitive Examination mainly in SSC, Railways and Banking. They involve using trigonometric ratios and formulas to calculate the height or distance of various objects, like buildings, mountains, or celestial bodies. These calculations have many practical applications in fields like architecture, astronomy, and surveying. This article provides a comprehensive overview of the concepts of heights and distances. It covers the relevant formulas, shows how to apply trigonometric principles, and walks through various problem-solving techniques. The information presented can be valuable for students as well as professionals working in related domains.
Heights and Distances Definition
Height is the measurement of vertical distance from any reference object while distance is the horizontal measurement of any particular point situated horizontally from the object. The height of the building, mountain, tower, flag, etc., and the distance between any two objects can be measured easily using trigonometric ratios and formulas.
You should know some important terms associated with height and distances to understand the concepts of heights and distances. The important terms of heights and distances are as follows:
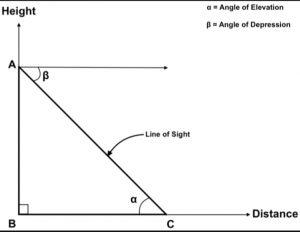
Line of Sight – The imaginary horizontal straight line drawn from the observer’s eye to the objects to be viewed. It gives an accurate idea of where the observers view.
Trigonometric Ratios – The sine, cosine, and tangent ratios that relate the sides and angles of a right-angled triangle.
Horizontal line – The line passing parallel to the ground or surface is called a horizontal line. The horizontal line is shown in the above figure.
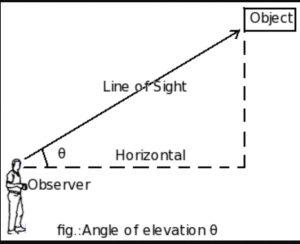
The angle of Elevation – The angle formed by the light of sight with the horizontal line when observers view the object situated upward over the horizontal line. It is formed only when the observer views the upward-placed object.
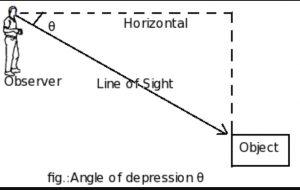
The angle of Depression – The angle of depression is the inclination of light of sight and horizontal line when observers view the downward object. It is formed only when the observer views the object at the ground from any height.
Heights and Distances Formula
The height and distance can be simply calculated using trigonometric ratios. Generally, the Tan trigonometric function is used to get height and distance accurately. We know that the ratio of the Tan function is tan = Height/Distance = Perpendicular/Base
You know the values of the tan function at different angles for this. The trigonometric values are mentioned in the table below. You can refer to the table for this.
Note: tan0°=0, tan30°=1/√3, tan45°=1
Heights and Distances in Trigonometry
Heights and Distances is a very broad application of trigonometry. Using this the distance between two or more objects or places and the height of the object by finding the angle subtended by two sides are found. The height and distance can be calculated using trigonometric functions. Trigonometry and its applications like heights and distances are used by architects, astronauts, surveyors, navigators, etc.
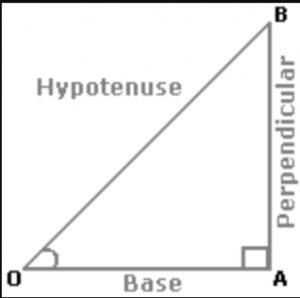
Trigonometric Ratios for various Angles
Sinθ = perpendicular/hypotenuse = AB/OB
Cosθ = base/hypotenuse = OA/OB
Tanθ = perpendicular/base = AB/OA
Cosecθ = 1/Sinθ = OB/AB
Secθ = 1/Cosθ = OB/OA
Cotθ = 1/Tanθ = OA/AB
Important Trigonometric Identities
- sin2θ + cos2θ= 1
- 1 + tan2θ = sec2θ
- 1+ cot2θ =cosec2θ
Problems on heights and distances
Que.1 From a point 350m away from the foot of the tower, the topmost point of the tower is observed by an observer making an angle of elevation of 45°. Find the height of the tower in meters?
Solution: In the right-angled triangle ABC, Tan45°=X/350, X=350m. So the height of the tower is 350m
Que.2 On the ground level the angle of elevation from the top of the tower is 30°. On moving 30m nearer to the tower the angle of elevation is 45° formed. Find the height of the tower?
Solution: Let the height of the tower is H30=h ⇒ (cot 30°- cot 60°)30=h ⇒(√3-1/√3)30√3=h ⇒(3-1) h=15√3.
Que. 3 Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
Solution: Let AB be the lighthouse and C and D be the positions of the ships.
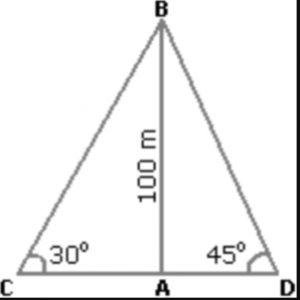
Then, AB = 100 m, ACB = 30° and ADB = 45°
AB/AC=tan30°=1/√3
AC = AB√3 = 100√3
AB/AD = tan45° = 1
AD = AB = 100m
CD = (AC + AD) = (100√3 + 100)m
= 100 (√3 + 1)
= 273m
Que.4 The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
Solution: Let AB be the wall and BC be the ladder
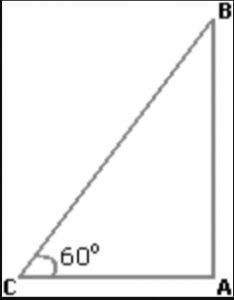
Then, ACB = 60° and AC = 4.6 m
AC/BC = cos60° = 1/2
BC = 2×AC
= (2×4.6)m
= 9.2m
Que.5 The angles of depression of two ships from the top of a lighthouse are 45° and 30° towards east. if the ships are 200 m apart, find the height of the light house.
Solution: Let us draw a figure below as per given question
Let AB = h meter be the height of the tower and two ships are situated at D and C respectively; such that, CD = 200 m; ∠ADC = 30° ∠ACB = 45° and BC = x meter (say)
Now from right triangle ABC,
tan 45° = h/x ⇒ 1 = h/x
∴ x = h
Again from right triangle ABD,
tan 30° = h/( 200 + x )
⇒ 1/√3 = h/( 200 + x )
Since x = h , we will get.
⇒ 1/√3 = h/(200 + h )
⇒ (200 + h ) = h X √3
⇒ h X √3 – h = 200
⇒ h x 1.732 – h = 200
⇒ h(1.732 – 1) = 200
∴ h = 200/0.732 = 273.2 m = 273 m
Que.6 At a point on a level plane a tower subtends an angle θ and a flag-staff a ft. in length at the top of the tower subtends an angle θ . The height of the tower is :
Solution: Let us draw a figure as per given question. Let OP be the tower of height h (say) and PQ the flag-staff of height a, such that ∠OAP = θ and ∠PAQ = Φ
In ΔOAP
Tanθ = P/B = Perpendicular distance / Base distance
⇒ Tanθ = OP/OA
⇒ OA = OP Cotθ
Put the value of OP in above equation, we will get
⇒ OA = hCotθ ……………. (1)
Now from triangle ΔOAQ,
⇒ Tan(θ + Φ) = OQ/OA
⇒ OA = OQ Cot(θ+ Φ)
⇒ OA = (h + a) Cot(θ + Φ) ………….(2)
from equation (1) and (2), We will get
∴ hCotθ = (h + a) Cot(θ + Φ)
⇒ Cotθ / Cot(θ + Φ) = (h + a) / h
⇒ Cotθ / Cot(θ + Φ) = h / h + a / h
⇒ Cotθ / Cot(θ + Φ) = 1 + a / h
⇒ (Cotθ / Cot(θ + Φ)) – 1 = a / h
⇒ (Cotθ – Cot(θ + Φ) ) / Cot(θ + Φ) = a / h
⇒ h = aCot (θ + Φ) / Cotθ – Cot(θ+ Φ)
After converting Cot into Sin and Cos, We will get
⇒ h = aSinθCos(θ + Φ)/SinΦ
Que.7 An observer 1.6 m tall is 20√3 away from a tower. The angle of elevation from his eye to the top of the tower is 30°. Find the height of tower?
Solution: Let observer be AB and tower be CD and BE is perpendicular to CD
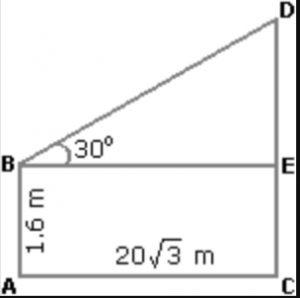
AB = CE = 1.6m
AC = BE = 20√3m
DE/BE = tan30° = 1/√3
then DE = 20√3/√3 m
= 20m
Since CD = CE + DE = 1.6 + 20
= 21.6m
Que.8 From a point P on a level ground, the angle of elevation of the top tower is 30°. If the tower is 100 m high, find the distance of point P from the foot of tower?
Solution: Suppose AB be a tower
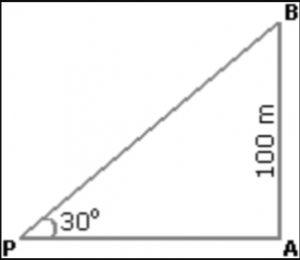
Angle APB = tan30° = 1/√3
AP = (AB×√3)m
= 100√3m
= 100×1.73
= 173m
Que.9 The angle of elevation of the sun, when the length of the shadow of a tree 3 times the height of the tower, is?
Solution: Suppose AB be a tree and AC be its shadow
Let angle ACB = θ
AC/AB = √3
Cot = √3
= 30°
Que.10 A man is standing on the deck of a ship, which is 10m above water level. He observes the angle of elevation of the top of a light house as 600 and the angle of depression of the base of lighthouse as 300. Find the height of the light house.
Solution: Let AB is the light house and the man is standing at C so, ∠BCD = 600 and ∠ACD = 300.
Let BD = h
In ΔADC, tan 300 = 10/CD
⇒ 1/√3 = 10/CD ⇒ CD = 10√3m
In ΔBDC, tan 600 = h/CD
⇒√3 = h/10√3
⇒ h = 30m
So the height of the light house is AB = AD + BD = 10 + 30 = 40m
Hope these study notes on Heights and Distances were helpful for you. If you want more notes like this then stay connected with sscadda.com. And if you want to read this article in Hindi then click on the link provided below.
Source link


