Area of Triangle
A triangle is a polygon, a 2-dimensional object with 3 sides and 3 vertices. Each polygon, irrespective of the number of sides can be divided into a number of triangles. The area of triangular shapes is determined by using a few simple formulae that are to be used while solving problems or questions. To find out the area, you must know the length of the sides, the type of triangle, and the height of the triangle. What is the formula to determine the area of Triangles? This post will answer all your queries related to the area of triangles.
Area of Triangle: Definition & Types of Triangle
A triangle is a two-dimensional polygon having 3 sides and 3 angles. The area of a triangle is the two-dimensional region occupied inside the triangle. A triangle can be of 4 types depending upon the length of its sides or the measure of its angles. The 4 types of triangles are:
- Right Angled Triangle- In which one angle is 90 degrees.
- Isosceles Triangle- In which 2 sides and 2 angles are equal.
- Equilateral Triangle- In which all the three sides are equal and hence each angle is of 60°
- Scalene triangle- In which all the three sides and angles are unequal.
Triangle Formula
The general formula for calculating the area of any triangle is given by 1/2 x Base x Height (Perpendicular). The other methods to calculate the area will depend upon the type of triangle as mentioned above. Let’s take a look at the formulae to find the area for each type of triangle.
Area of Right Angled Triangle Formula
A right-angled triangle is a triangle in which one angle is 90°. The relation between the sides and angles of a right-angled triangle is the basis for trigonometry. The side opposite the right angle is the hypotenuse. The formula to determine the area of the right-angled triangle is given below.
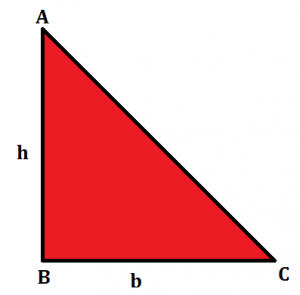
In the right-angled triangle given, we have the perpendicular as ‘h’ and base as ‘b’ So the formula for the area of a right-angled triangle can be given by:
Area of a right-angled triangle = 1/2 x b x h
- In some cases, the length of the hypotenuse and either base or height is given. In that condition, you will have to find the length of the remaining side using the Pythagoras theorem.
Area of Isosceles Triangle Formula
In an isosceles triangle, you will have 2 sides of equal lengths. Hence, the 2 angles of this triangle will be equal to one another. In the figure given below, we have an isosceles triangle with two equal sides, ‘a’ and the base as ‘b’. A perpendicular is drawn from A to D which divides the base into 2 equal parts.
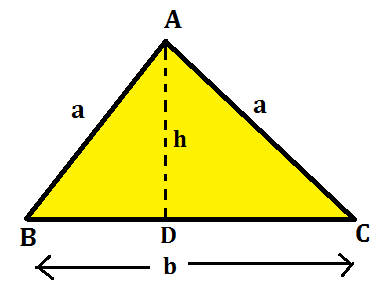
The measure of the height of the triangle can be calculated using the Pythagoras theorem as the Triangle ADC is a right-angled triangle.
h = √a²-(b/2)² = 1/2 x (√4a²-b²)
Hence, by the formula, A = 1/2 x b x h, we can derive the formula for the area of the isosceles triangle by the formula given below:
Area of isosceles triangle = 1/4 x b x √4a²-b²
Area of Equilateral Triangle
In an equilateral triangle, you will have the 3 sides of equal lengths. Hence, all the 3 angles of this triangle will be equal and of 60 degrees. In the figure given below, we have an equilateral triangle with equal sides as ‘a’. A perpendicular is drawn from A to D which divides the base into 2 equal parts.
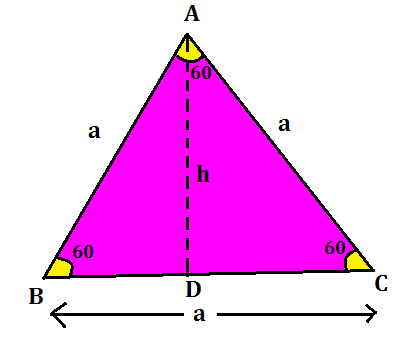
Here also the height of the triangle will be calculated using the Pythagoras theorem.
h = √(a²-a²/4) = √3/2 x a
Hence, by the formula, A = 1/2 x b x h, the formula for the area of the equilateral triangle can be derived as:
Area of Equilateral triangle = 1/2 x (a x √3/2 a) = √3/4 x a²
Area of a triangle by Heron’s Formula
A scalene triangle is a triangle in which all the 3 sides are unequal and no angle is 90 degrees. To find the area of a scalene triangle and even other triangles, we use Heron’s Formula. The formula given by Heron about the area of a triangle is also known as Hero’s formula.
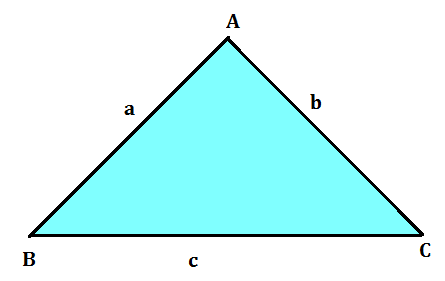
From the figure given above, a scalene triangle is given with 3 sides as ‘a’, ‘b’, and ‘c’. Heron’s formula is stated as:
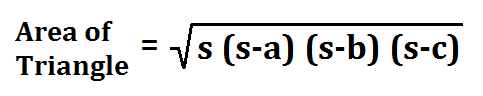
where a, b and c are the sides of the triangle, and s = semi-perimeter, i.e., half the perimeter of the triangle. The semi-perimeter of the triangle is given by:
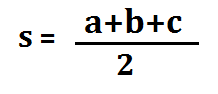
This Heron’s Formula can be applied to any type of triangle i.e. Right triangle, Isosceles triangle, Equilateral triangle and Scalene triangle. If anyone calculates the area of an equilateral triangle, it will be the same either by Heron’s Formula or by using the specific formula i.e. √3/4 x a².
Area of a triangle by Using The Measure of Angle
In some cases, the length of two sides of a triangle and the measure of the angle contained between them has been provided and the area of the triangle is asked to be calculated. If we consider the length of the two sides be ‘a’ and ‘b’ and the measure of the angle to be x degrees, the area of the triangle in such a case will be:
Area of the triangle = 1/2. a . b. sinx
Area of Triangle: Examples
Example 1: Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm.
Solution: Here we have the perimeter of the triangle = 32 cm, a = 8 cm and b = 11 cm.
Third side, c = 32 cm – (8 + 11) cm = 13 cm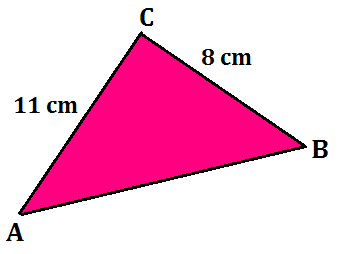
So, 2s = 32, i.e., s = 16 cm,
s – a = (16 – 8) cm = 8 cm,
s – b = (16 – 11) cm = 5 cm,
s – c = (16 – 13) cm = 3 cm.
Therefore, the area of the triangle =
√16 x 8 x 5 x 3 = 8√30 cm²
Example 2: Find the area of a right-angled triangle with a base of 14 cm and a height of 5 cm.
Solution: Area of a right-angled triangle = 1/2 x b x h
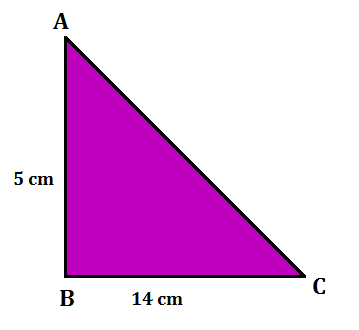
Hence, the area of the right-angled triangle is
A= 1/2 x 14 x 5 = 35 cm²
Source link


